Introduction
Kirchhoff’s Voltage Law (KVL) is one of the most important fundamental laws used in electrical circuit analysis. The German physicist Gustav Robert Kirchhoff proposed this law in 1845, and he based it on the principle of conservation of energy. It explains how voltages behave in a closed electrical loop and forms the foundation for analyzing electrical and electronic circuits. KVL is applicable to both AC and DC circuits.
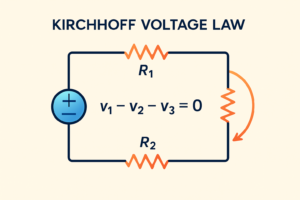
What is Kirchhoff’s Voltage Law?
Kirchhoff’s Voltage Law states that:
➤ In any closed loop of an electrical circuit, the algebraic sum of all voltages is zero.
In simpler terms, the total voltage supplied in a closed loop equals the total voltage drop across the components in that loop. This means that sources completely use the energy supplied by the circuit elements.
Mathematical Expression of KVL
KVL can be expressed mathematically as:
ΣV = 0
Or equivalently:
ΣVrise = ΣVdrop
- Vrise = voltage sources
- Vdrop = voltage drops across circuit elements
Principle Behind Kirchhoff’s Voltage Law
Kirchhoff’s Voltage Law derives from the law of conservation of energy, which states that energy can neither be created nor destroyed. In a closed electrical loop, the voltage sources must supply energy equal to the energy consumed by resistors and other components.
Understanding KVL with a Simple Example
Consider a closed loop circuit containing a 12 V battery and two resistors with voltage drops of 5 V and 7 V.
+12 V − 5 V − 7 V = 0
This confirms the validity of Kirchhoff’s Voltage Law.
Sign Convention in Kirchhoff’s Voltage Law
- Voltage rise (from negative to positive terminal of a source) is taken as positive
- Voltage drop (in the direction of current flow across a component) is taken as negative
Maintaining a consistent sign convention is essential for correct circuit analysis.
Step-by-Step Procedure to Apply KVL
- Select a closed loop in the circuit
- Assume a direction for loop current
- Traverse the loop in the assumed direction
- Assign voltage rises and drops using sign convention
- Apply KVL: ΣV = 0
- Solve the equation to find unknown values
Applications of Kirchhoff’s Voltage Law
- Loop (mesh) analysis
- Series circuit voltage calculations
- Electronic circuit design
- Power supply and amplifier analysis
- Electrical power systems
Practical Example: Series Circuit
Consider a series circuit with a 10 V source and three resistors having voltage drops of 2 V, 3 V, and 5 V.
10 V = 2 V + 3 V + 5 V
This shows that the supplied voltage equals the total voltage drop.
Kirchhoff’s Voltage Law in AC Circuits
Kirchhoff’s Voltage Law also applies to AC circuits when circuits represent voltages as phasors. In such cases, engineers apply KVL using complex numbers to account for phase differences between voltages across resistors, inductors, and capacitors.
Limitations of Kirchhoff’s Voltage Law
- Assumes lumped circuit elements
- Less accurate at very high frequencies
- Does not consider electromagnetic radiation losses
- Not valid in circuits with time-varying magnetic fields
Difference Between KVL and KCL
| Aspect | KVL | KCL |
|---|---|---|
| Deals with | Voltage | Current |
| Applied to | Closed loop | Node |
| Based on | Conservation of energy | Conservation of charge |
| Equation | ΣV = 0 | ΣI = 0 |
Advantages of Kirchhoff’s Voltage Law
- Simple and systematic approach
- Applicable to AC and DC circuits
- Helps analyze complex electrical networks
- Essential for troubleshooting and design
Real-Life Analogy of KVL
Kirchhoff’s Voltage Law can be compared to walking around a hill and returning to the starting point.The total height gained equals the total height lost, resulting in zero net change—similar to voltage rise and drop in a closed electrical loop.
Conclusion
Kirchhoff’s Voltage Law is a fundamental principle that helps understand voltage distribution and energy conservation in electrical circuits. By applying KVL to closed loops, complex circuits can be simplified and analyzed efficiently. Along with Kirchhoff’s Current Law, KVL forms the backbone of electrical circuit analysis.